Out of the beaten path: Lundberg’s take on instability

The idea that the economy can be fluctuating even if markets are at equilibrium (all which is produced is sold) was built into early macro-dynamic models. This is apparent in the models developed by Tinbergen (1934), Kalecki (1935) or Samuelson (1939a,b), where at any point of time the whole production is sold; instead, the movement of the economy stems from the existence of various delays responsible for keeping the economy away from its stationary state. Erik Lundberg pointed to another direction when he published his Studies in the Theory of Economic Expansion (1937). The question he asked was: How would the economy behave when pushed outside of its market equilibrium? At a time when this approach was still exploratory in economic models, his was a groundbreaking study.

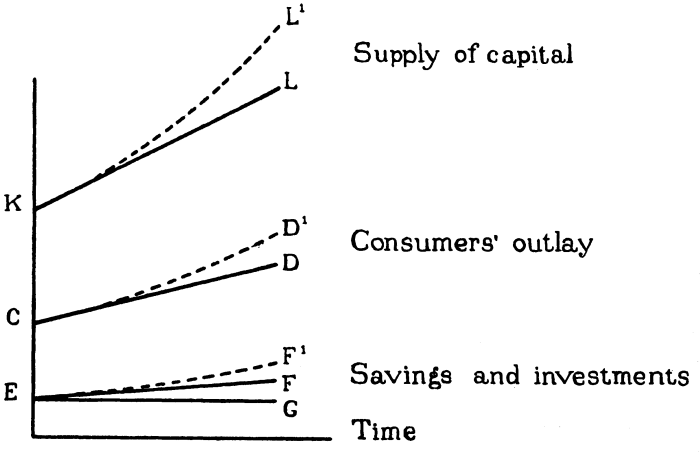
Lundberg illustrated in this figure (1937: 183) the necessary condition for the “dynamic equilibrium”: the development of economic variables must be exponential rather than linear

With that aim in mind, Lundberg examined the conditions for which an economy may grow steadily and then wondered what would happen if these conditions were not fulfilled. His first step was to show on the basis of a small model (Lundberg, 1937: 185, reproduced hereafter) that the development of investment and capital was necessarily exponential, and that a linear development would lead to imbalances in the economy. Consider a model where a fraction $\Lambda$ of income is saved at every moment. Assume that $\Lambda$ is equal to 0.2, and that production $Y$ is equal to 100 units. Then, if 80 units are consumed, for the equilibrium to be obtained, 20 units need to be invested. Suppose now that there is a fixed relationship between investment and the variations of production such that $I=\mu \dot Y$ with for instance $\mu=2$ . Assuming no depreciation of the stock of capital, we have $K=\mu Y$ . With the condition that $I=S$ at each point in time, we obtain the differential equation $\dot Y= \frac{\Lambda}{\mu} Y$ which represents the model economy, and the solution $Y=ce^{\frac{\Lambda}{\mu}t}$ , where $c$ is a constant determined by the initial conditions of the economy. With the values $\Lambda=0.2$ and $\mu=2$ , this means that the economy will grow at a rate of $\frac{\Lambda}{\mu}=0.10$ , a “dynamic equilibrium.”

But Lundberg questioned the possibility of this continued expansion: “Production, consumption, income, savings, and investments are all increasing at certain rates, and we ask whether this growth can continue in some sort of dynamic equilibrium, or whether discrepancies must automatically come into being within the system itself, which have the tendency to interrupt the process” (Lundberg, 1937: 183). For him, the problem comes from the assumed equality between investment and savings: “This equilibrium condition must be disrupted, in order to explain or analyse a development.” Investment must be explained “causally” and not simply assumed to be at its necessary level to offset savings, and this led Lundberg to suggest that “If due regard is paid to the determining factors of investment, the tentative straight-line solution might give a more accurate picture of the system’s inherent tendencies toward discrepancies than the equilibrium solution giving exponential curves” (Lundberg, 1937: 186).

What happens now if the economy is off this balanced trajectory? What happens for instance if what is produced is not sold? Is the economy likely to get back on its initial track? Shall we instead expect to see the disequilibria growing over time? Here are the questions raised by Lundberg and the meaning of the various “sequences” he attempted to build in his book. Lacking the mathematical skills of his fellow economists from the Econometric society, Lundberg fell short of producing alternative mathematical models. However, in pointing in a new direction giving a central role to market disequilibria, he undoubtedly influenced the future direction of research which paid more and more attention to those issues from the 1940s onward.

References:

Kalecki, M. 1935. “A Macrodynamic Theory of Business Cycles.” Econometrica 3(3):327–44. https://www.jstor.org/stable/1905325

Lundberg, Erik. 1937. “Studies on the theory of economic expansion.” Stockholm: Kungl. Boktryckeriet. P. A. Norstedt & Söner

Samuelson, Paul A. 1939a. “A Synthesis of the Principle of Acceleration and the Multiplier.” Journal of Political Economy 47(6):786–97. https://www.jstor.org/stable/1824312

Samuelson, Paul A. 1939b. “Interactions between the Multiplier Analysis and the Principle of Acceleration.” The Review of Economics and Statistics 21(2):75–78. https://www.jstor.org/stable/1927758

Tinbergen, Jan. 1934. “Der Einfluß Der Kaufkraftregulierung Auf Den Konjunkturverlauf.” Zeitschrift Für Nationalökonomie / Journal of Economics 5(3):289–319. https://www.jstor.org/stable/41792889