This post is based on some parts of chapter 4 of the book. All comments are welcomed.
“Well, in OUR country,” said Alice, still panting a little, “you’d generally get to somewhere else — if you ran very fast for a long time, as we’ve been doing.” “A slow sort of country!” said the Queen. “Now, HERE, you see, it takes all the running YOU can do, to keep in the same place. If you want to get somewhere else, you must run at least twice as fast as that!” (https://victorianweb.org/authors/carroll/zrd/2.htm)
In the early 1930s, Kalecki wrote a series of papers culminating with the publication of his Essay on the Business Cycle Theory (1933). In these works, he developed a specific vision of an asymmetric world where capitalists had in their hands the whole fate of the economy. This was true when capitalists were taken as a class, in accordance with the idea that they earned as much as they spent. As an individual, however, the lone capitalist did not have any control over the decisions taken by others and eventually to what happened to him.
A mathematical version of this Essay was presented at the third European meeting of the econometric society, in Leiden in 1933. In his communication, Kalecki managed to account for the situation described in the Essay on the basis of a mathematical tool introduced by Jan Tinbergen (1931). The model comprised four equations. Solving it analytically, Kalecki showed that, with a rough estimation of the parameters (the parameters m and n being the coefficients of the investment function and representing the time to build for investment goods), his model led to the existence of sustained, endless oscillations, of a period similar to the decade-long duration that was then observed and still prevails today.
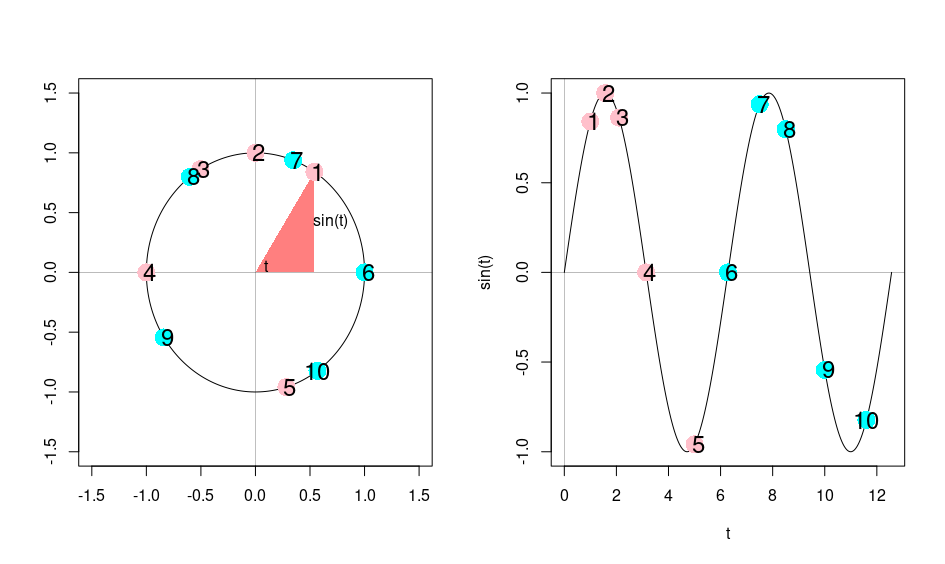
The metaphor of “running on the spot” introduced by Lewis Carroll in his novel Alice Through the Looking-Glass fits well with that picture. As the “Red Queen” who was surprised not to move an inch as she ran, capitalists caught up in the race for more profits are proving incapable of having any lasting impact on the world. The sustained cycle represented by a sinusoidal function is actually the mathematical translation of this idea of an infernal circle, which can easily be seen if we represent this function as one coordinate of a circle, which repeats endlessly. At the end of the cycle, it is important to understand that the model goes back to its original point, the productive capacities and the national income having not varied. This demonstrated for Kalecki that the unrestrained pursuit of profits eventually left the world unchanged, stagnant.
The circle should be read in the counterclockwise direction, on the right we represent the sine function as a function of time ‘t’, where ‘t’ can also be seen as the angle in the circle between the horizontal axis and a line drawn from the origin to a point on the circle.
In addition, the model highlighted that the movements of the economy were independent of the power that capitalists can exercise within their own organization or in what Marx called the “sphere of production.” This is because in Kalecki’s world, profits originate in the “sphere of circulation” where goods are sold and profits are realized. For that very reason, a rise in profit margin (or “markup”) is never the result of a struggle to the advantage of the capitalists to get a larger amount of profits as it is the case for Marx. As long as capitalists earn as much as they spend, such a movement comes with employment and output adjustments but no change in the level of profits: capitalists simply earn a new share of a new GDP. Politically, on the other hand, class struggle can have a considerable role insofar as it can guide economic, diplomatic and military policy. It is only in this indirect way that they can influence the level of the economy.
We can illustrate in this application the effect of a change in the profit share, based on Kalecki’s own equations in the Polish Essay.
Kalecki express the profit in terms of the profit share and the degree of utilization of the capital stock
We pose that 
, that is the profit share is constant so that 
. This equation for 
determines a line in the (Y,P) plane which corresponds to the potential profits that the firm could make if it managed to sell the whole of its production. In accordance with Kalecki’s theory of profit, the profits that the firm realizes are determined by capitalists’ spendings. This can be seen if one expresses the aggregate income in terms of wages and profits on one side and consumption and accumulation on the other side so that 
. Since Kalecki assumes that all wages are consumed and that capitalists consumes a small fraction of their profits (
), one gets the equation of profits below.
Equating both equations for P, we obtain an equation for Y as a function of A:
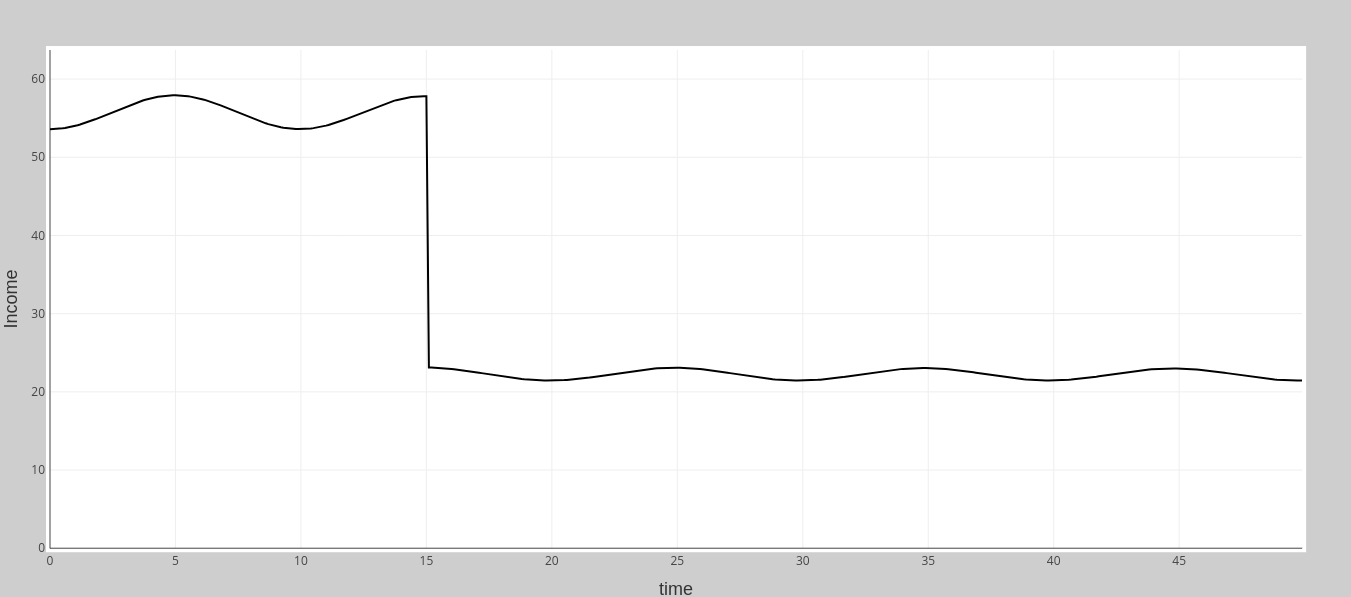
This gives us the dynamic of national income which shows that after a shock on c (change in the profit share) the income will adjust to a new level (see the “Income” panel in the application above), while the profit rate 
remains unchanged (panel “Profit rate”).
At the Leiden meeting, Fisher urged his fellow econometricians to look at things from a different perspective and to contemplate the possibility that the economy may be stable only in the neighborhood of its stationary state (Fisher, 1933). At this particular conjuncture, while the crisis showed no sign of ending, Tinbergen was the first to take the bait and to question the idea of stability. He soon pushed forward a new approach with the idea that there may be multiple equilibria in the economy, and that some of them may be unstable and lead to a complete or partial collapse. Frisch, against all odds but also in reference to Fisher, proposed to integrate this idea in his own models as well. But this was not the case for Kalecki who “stood by his guns” to use Samuelson’s words.