This post is based on a working paper accessible here. All comments are welcomed.
At the turn of the 1920s-1930s, dynamic economic models formulated mathematically were still a scarce resource. However, a lot of efforts were put into finding an approach able to represent the facts that had been shown by the explosion in empirical findings during the previous decade. One of this findings was that the amplitude of fluctuations would vary very little; another was that the periodicity of fluctuations, in spite of all the efforts of smoothing the data, was not entirely regular: some booms were shorter, some depressions lasted longer, and there was an asymmetry between boom and bust that was well-known.
To capture these properties in a single model, the Dutch engineer Ludwig Hamburger, who dabbled in building economic models during this period (Hamburger, 1930; 1931), was inspired by the recent work of another Dutch, the physicist Balthasar van der Pol (1926; 1928; 1930), who had formulated a general nonlinear equation that was able to explain many physical, electrical and even mechanical phenomena. He dubbed his equations “relaxation equations”, and Hamburger imported almost word for word his presentation of their behavior, to apply it to economic cycles.
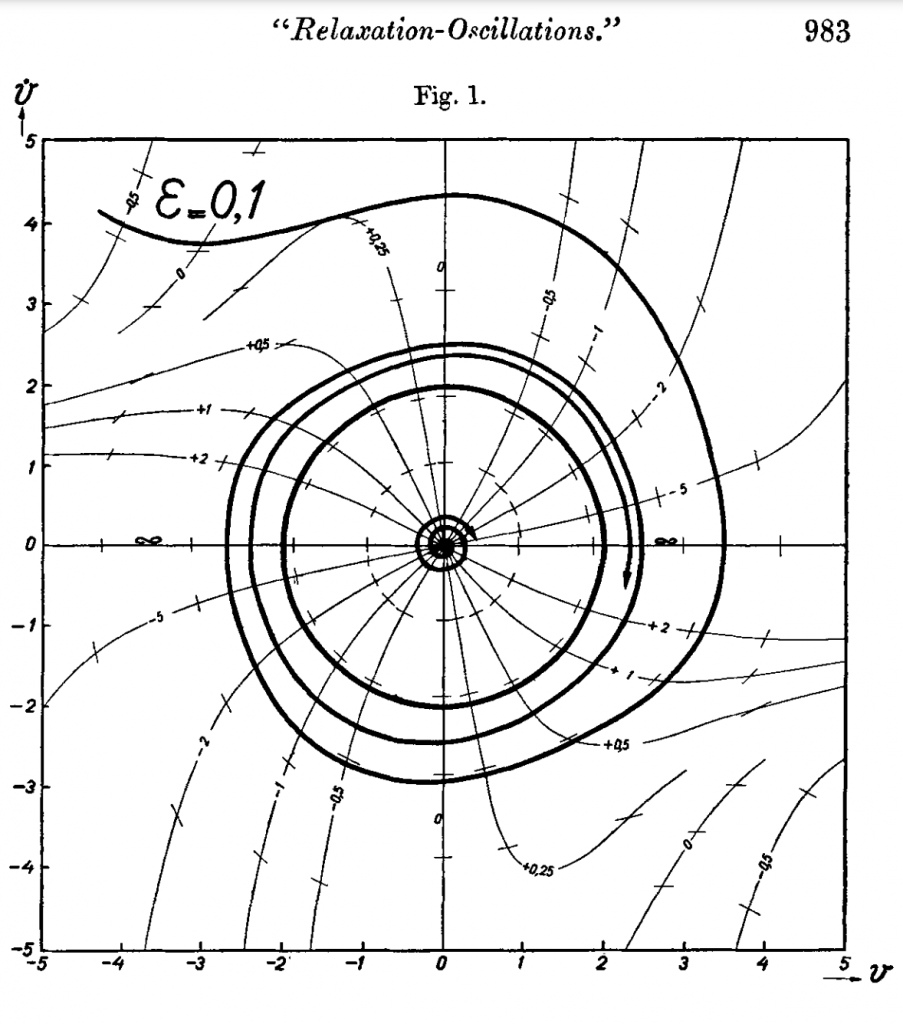
The crux of the equation was that its resistance coefficient (
) was non-linear. After a perturbation of the equilibrium, the amplitude of fluctuations would grow more or less slowly according to a parameter 
, and once it reached a certain value, it would stop growing and enter a limit cycle:
Another important characteristic of this equation is that once reached a certain value, the form of the fluctuations is transformed into a non-sinusoidal vibrations with sudden “charges” or “discharges” phenomena. Indeed, once the variable reached a ceiling or floor, it would slowly drift away from it, until a breaking point was reached and it jumped to a high or low value.
Although Hamburger took up most of his mathematics and even interpretations from van der Pol, it should be noted that it was a case of non-mechanical analogy, because Hamburger rejected the approach of the pendulum, and van der Pol had himself applied his findings to biological problems such as the heartbeat. Hamburger was also particularly interested in the effect of shocks on this system, and although he did not present a simulation of their effect, he did understood that they would change the period rather than the amplitude of the fluctuations, and based his interest for them on this particular characteristic. The following application reproduces a simple van der Pol oscillation based on the equation above, and allows the user to add a shock that is normally distributed with mean 
and standard deviation 
.
Hamburger’s ideas were originally well-received among the nascent Econometric Society; Ragnar Frisch, the founder and main driver of the society, had worked (Frisch, 1928) on the problem of understanding time series where the periodicity was changing, and he wrote to Hamburger that his explanation mixing shocks and relaxation oscillations was far superior. Hamburger was thus invited to the early meetings of the Econometric Society, however he failed to convince other econometricians and macrodynamists for at least three reasons.
The first was that there were other progress being made on dynamic economic models, that outpaced the solution proposed by Hamburger and gave a new meaning to shocks and the source of oscillations. It was in particular Tinbergen (1933), Kalecki (1935) and Frisch (1933) who were able to build determinate models based on truly economic relationships, something that Hamburger never quite managed to do. A second reason was that the problem tackled by the macrodynamists began to change with the deepening of the depression: in the years around 1933-35, Frisch and especially Tinbergen built models that showed the possibility of a radical instability, a collapse of the economy instead of limit cycles around an equilibrium position (two other posts on this blog describe Tinbergen’s approach to the problem, here and there). Finally, the idea presented by Frisch in 1933, that the economic oscillations were damped and periodically revived by external impulses, became the dominant approach to self-sustained oscillations, which contributed to the abandonment of the line of research advocated by Hamburger.
However, the approach was revived a few years later; by a twist of fate, it was through Philippe le Corbeiller, a French engineer who had also been invited to give his take on relaxation oscillations in the early 1930s, that those equations came back to economics in the early 1950s. At that time, le Corbeiller was a physicist at Harvard University, where he met Richard Goodwin and convinced him of the interest for economics of these equations. Where Hamburger had failed to build a truly economic model, Goodwin succeeded in the midst of a renewal of interest in nonlinear cycle theory, and his model had a lasting impact on business cycle studies.
References:
Link to our WP: